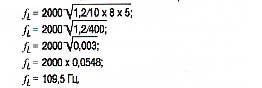Теория проектирования студий
Звуковая волна
Что же представляет собой звуковая волна? Звук состоит из множества локальных изменений плотности воздуха, которые волнообразно распространяются в воздушной среде с определенной скоростью, называемой скоростью звука. При обычной комнатной температуре скорость звука составляет около 340 м/с, а ее незначительные отклонения зависят главным образом от температуры воздуха. На всех частотах звуковая волна распространяется практически с одинаковой скоростью. Скорость звука обозначается в формулах символом «c».
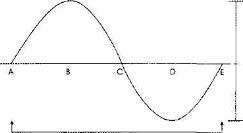
Одними из главных характеристик звуковой волны являются ее длина (определяемая количеством периодов/циклов изменения давлений за единицу времени), амплитуда (максимальная разница между самым высоким и самым низким давлением внутри одного цикла), форма волны и пр.Расстояние, которое звуковая волна проходит со скоростью звука за один цикл на определенной частоте, называется длиной волны. Под полным циклом подразумевается повышение давления воздуха, прохождение его через точку наибольшего давления, затем понижение давления, прохождение через «нулевую отметку», дальнейшее понижение давления с прохождением через точку максимального разрежения, а затем повышение давления до исходной величины. Таким образом, один цикл включает в себя два полуцикла: давления и разрежения (рис. 1). Длина волны измеряется в метрах (дециметрах, сантиметрах), а в формулах обозначается символом «л» (лямбда).
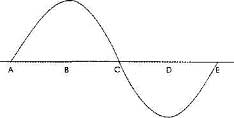
Рис. 1. Звуковая волна синусоидальной формы: В — точка наивысшего давления; D — точка максимального разрежения; А-С — полуцикл давления; C-D — полуцикл разрежения.
Количество полных циклов изменения давления за единицу времени называется частотой. Частота звуковой волны измеряется в количестве полных циклов за секунду, а именно — в герцах. В формулах частота обозначается символом «f».
Между длиной волны, частотой и скоростью звука существует взаимосвязь, которая выражается простой формулой л = с\ f. Другими словами, длина волны равна скорости звука, поделенной на частоту. Например, нам нужно определить длину волны на частоте 100 Гц. Подставляем значения в формулу: л = 340 :100 = 3,4 м. А чтобы не прибегать постоянно к формуле, можно довольно быстро составить небольшую таблицу, отображающую соотношение частоты к длине волны.
Распространение звуковой волны и фаза.
Как же происходит распространение звуковой волны в помещении? Распространяясь в помещении от своего источника (громкоговорителя, музыкального инструмента и пр.), звуковая волна расширяется до тех пор, пока не достигнет граничных поверхностей этого помещения: стен, пола, потолка и т.д. Часть энергии звуковой волны (особенно в низкочастотном диапазоне) проходит сквозь стены, часть поглощается внутри стен, а часть отражается обратно внутрь помещения. В разной степени все три вида распределения звуковой энергии присутствуют практически во всех случаях, но мы здесь остановимся на последнем.
Отраженная звуковая волна, потеряв часть энергии, изменит направление и будет распространяться до тех пор, пока не достигнет других поверхностей помещения, от которых она снова отразится, потеряв при этом еще часть энергии, и т.д. Так будет продолжаться до тех пор, пока энергия звуковой волны окончательно не угаснет. Если, например, в пустом помещении включить пару громкоговорителей, то звук от них начнет сталкиваться с поверхностями помещения и перемещаться по очень сложным траекториям. На слух это будет восприниматься так: сначала мы услышим прямой звук непосредственно от громкоговорителей, спустя несколько миллисекунд в прямой звук «вмешаются» первые (и самые сильные) отражения от поверхностей, а еще через какое-то время этих отражений (хотя и намного более слабых) будет великое множество. Собственно, их мы и называем реверберацией. Кстати, рассеивание звуковой энергии в помещении представляет собой превращение ее в основном в тепловую энергию из-за сопротивления воздуха и вследствие каждого соприкосновения с поверхностями стен. Не по этой ли причине в студиях с хорошим звукопоглощением часто бывает так жарко?
Но прежде мы рассмотрим «поведение» ранних отражений и те эффекты, которые они производят. Звуковая волна при столкновении с поверхностью частично отражается под тем же углом, под которым падает на эту поверхность, но ее фаза при этом не изменяется. Что такое фаза? Представим себе окружность, протяженность периметра которой равна расстоянию между точками А и Е (рис. 1 и 2), другими словами, равна длине волны на определенной частоте. По мере «вращения» этой окружности ее радиальная линия в каждом отдельно взятом месте синусоиды будет находиться на определенном угловом расстоянии от начальной точки, что и будет значением фазы в каждой такой точке. Фазу измеряют в градусах, реже — в радианах. Один радиан — это угол, при котором окружность «провернулась» на длину своего радиуса. Поэтому 360° = 2п радиана (другими словами, длина окружности равна 2п, умноженное на значение радиуса). Отсюда 1 радиан = 360\2п = примерно 57,3°.
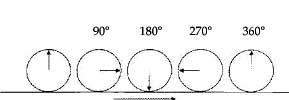
направление вращения окружности Рис. 2. Синусоидальная волна; амплитуда и фаза. Если протяженность периметра окружности равна одному циклу синусоиды (расстояние от А до Е), то по мере вращения радиальная линия этой окружности будет показывать угол, который соответствует значению фазы синусоиды в конкретной точке.
Большинству из нас известно, что изменение фазы на 180″ приводит к изменению полярности. Поэтому, если смешать два сигнала одинаковой частоты и амплитуды, но несовпадающих на 180° по фазе, то они будут взаимопогашаться. Поворот фазы сигнала на 360 или 720° равен соответствующему количеству полных циклов, а это означает возврат к нулевому значению фазы. Итак, мы уже говорили, что при столкновении звуковой волны с поверхностью фаза звуковой волны не изменяется. Мы также выяснили, что между расстоянием, пройденным звуковой волной, и фазой существует зависимость. А это значит, что при достижении граничной поверхности фаза звуковой волны зависит от расстояния от источника звука до поверхности и от частоты этой звуковой волны. На рис. 3 можно увидеть, как волны с различной частотой, распространяемые от одного источника, доходят до отражающей поверхности с различной фазой. Фазу отраженной звуковой волны можно рассчитать из суммарного расстояния, которое прошла волна от своего источника до граничной поверхности и обратно. Если это суммарное расстояние, разделенное на длину волны, дает целое число, то фаза волны в начале и в конце ее пути совпадает.

Рис. 3. Фазовая зависимость отраженных волн. Звуковые волны на разных частотах (а, значит, и разной длины), излучаемые источником звука с одной и той же фазой, после прохождения одинакового расстояния достигают поверхности с разной фазой.
Моды и резонансы
Когда две граничные поверхности параллельны, то звуковая волна отражается от одной из них в направлении другой, затем снова в обратном направлении, и так много раз до тех пор, пока не рассеется ее энергия. И если расстояние между граничными поверхностями -от источника звука к первой поверхности, затем ко второй и обратно к источнику — является кратным длине волны, то возвращающаяся волна будет такой же по фазе, что и исходящая волна. В результате их взаимодействия энергия звуковой волны на этой частоте будет усиливаться. Это явление называется резонансом. Резонансы могут возникать также вследствие отражения от множества поверхностей. Главное в том, чтобы звуковая волна в конечном итоге возвращалась в исходную точку с той же фазой, с какой она была в момент излучения. Трудно представить, сколько возможных комбинаций, порождающих резонансы, может быть в самом обычном помещении.
Некоторые из таких отражений снова и снова проходят назад и вперед по одному и тому же маршруту и становятся резонансными модами. Существует три основных типа резонансных мод, которые склонны к нарастанию и самоусилению. Осевые моды возникают между двумя параллельными поверхностями и распространяются параллельно другим четырем поверхностям любого помещения в форме параллелепипеда (четыре стены, потолок и пол). Тангенциальные (касательные) моды «ходят» по кругу, касаясь четырех поверхностей, и остаются параллельными двум остальным поверхностям. Косые (наклонные) моды «гуляют» между всеми шестью поверхностями комнаты и не распространяются параллельно ни одной из них.
Если мы представим, что в помещении ничто не поглощает энергию звуковой волны, то короткий широкополосный импульс от источника звука будет распространяться в помещении непредсказуемо. Звуковая волна будет распространяться по самым многочисленным маршрутам, но усиливаться будут только те частоты и на тех маршрутах, которые соответствуют резонансным частотам, а все остальные быстро угаснут. В результате мы получим звуковое поле, которое будет представлять собой сумму возбужденных резонансов. Эти резонансные направления называются естественными модами помещения, а резонансные частоты — естественными частотами помещения (айген-тонами). Естественные моды и естественные частоты помещения определяются только его геометрическими размерами и свойствами.
В предыдущем абзаце мы умышленно рассмотрели случай, когда внутри помещения отсутствует звукопоглощение. Сделано это было для того, чтобы яснее продемонстрировать возникновение естественных мод и естественных частот помещения. Если же поверхности помещения имеют звукопоглощающие свойства, то резонансные моды по-прежнему существуют, однако энергия звуковой волны затухает быстрее и скорость этого затухания зависит от степени звукопоглощения. Для поддержания в звукопоглощающем помещении уровня звука на заданной отметке источник звука должен постоянно генерировать звук на уровне, который зависит как от наличия в помещении возбужденных резонансных мод, так и от степени звукопоглощения поверхностей помещения.
Если в звукопоглощающих условиях источник звука издает короткий одиночный сигнал, это приводит к возбуждению многочисленных маршрутов его движения. Но через короткий период «выживают» только резонансные моды, а помещение продолжает какое-то время «гудеть» на резонансных частотах до тех пор, пока моды не затухнут полностью. Кстати, время, за которое энергия звуковой волны затухает на 60 дБ по отношению к своему исходному уровню, называется временем реверберации. Измеряется оно как средняя скорость затухания звука в помещении с момента резкого прерывания работы постоянно действующего источника звука. Детальнее о времени реверберации — чуть позже.
По мере увеличения степени звукопоглощения поверхностей комнаты уровень звука на резонансных частотах, а «частотная полоса» каждой моды (диапазон частот, в котором мода может более или менее возбуждаться) увеличивается. И если представить, что поверхности стен обладают 100%-ным звукопоглощением (например, безэховая камера), то в этом случае будут отсутствовать даже первые отражения звуковой волны. А если это так, то пропадают и маршруты этих отражений, а значит моды прекращают свое существование.
Таким образом, значительная часть этой статьи будет посвящена модам, резонансам и их распределению в помещении. И это не удивительно, так как именно они в основном и определяют акустические особенности любого помещения. А требования к студийным помещениям в этом смысле являются очень высокими. Когда в помещении раздаются звуки, например речь или музыка, уровень непрерывных слагающих звучания зависит от того, совпадают ли они с какими-нибудь возбужденными резонансами помещения или нет. Импульсные же слагающие звучания — уже после того, как исчезает сам импульсный сигнал,- «зависают» на резонансных частотах. Это может проявляться в виде неразборчивости вокала, бубнения, нежелательной окраски звучания инструментов и т.д., что в студиях, мягко выражаясь, не приветствуется.
Тему, которую мы сейчас затронули, мы и дальше будем расширять по ходу нашего повествования. В каком бы направлении мы ни двигались в поисках путей создания достойной акустики студийных помещений, наша задача всегда будет сводиться к необходимости подавления резонанса помещений. Именно так мы сможем добиться того, чтобы помещения обладали нужным нам уровнем «музыкальности» и сполна отвечали нашим целям. Мы, в конечном счете, должны добиться такого звучания, которое бы нас устраивало и не определялось преобладанием собственных резонансных частот помещения. Наиболее очевидными здесь представляются два направления. Во-первых, это варианты изменения геометрии помещений; в этом случае мы можем поставить под свой контроль траекторию распространения волн, а значит и резонансные моды и их частоты. Во-вторых, применение звукопоглощающих конструкций; это позволит нам добиться контроля как над уровнем отражений, так и над распространением звуковых волн тех частот, которые усиливают энергию конкретных мод.
Поэтому я предлагаю далее рассмотреть эффект геометрического конфигурирования помещений, влияние звукопоглощающих конструкций, а также частотное распределение естественных резонансов помещения
Геометрическое конфигурирование помещений
Эффект геометрического конфигурирования помещения состоит в изменении углов между стенами, их размера и количества, а также пропорций между размерами стен. Нам уже ясно, что геометрически параллельные поверхности способствуют возникновению осевых мод. Из всей совокупности резонансных мод (осевых, тангенциальных и косых) именно осевые за счет отражений между параллельными стенами способствуют возникновению самых сильных резонансов. Понятия параллельности в акустическом и геометрическом смысле слова — разные, и понятие акустической параллельности зависит не только от геометрической параллельности, но и от частоты отражаемой между поверхностями звуковой волны. Этот вопрос хорошо освещен в книге Филипа Ньюэлла «Recording Spaces'», a размышления автора на эту тему приводятся ниже.
«На рис. 4 показаны две отражающие стены длиной по 10 м с расстоянием между ними тоже в 10 м. Они параллельны геометрически, а поэтому являются параллельными и акустически на всех частотах. Хлопок в ладоши в точке X рождает звук, содержащий очень много частот, и этот звук будет распространяться от источника во всех направлениях. Волны, ударяющиеся в точках Y и Z, будут отражаться назад, проходя через позицию источника, «гуляя» туда и обратно вдоль линии Y-X-Z. Частоты, длина волн которых кратна расстоянию между точками Y и Z, будут проходить по положительным и отрицательным пикам давления в тех позициях в помещении, которые совпадают по каждому отражению. Они будут возбуждать резонансные моды, сильно усиливающие друг друга и ощущающиеся на слух, как правило, в каких-то отдельных точках помещения, не проявляясь при этом в других местах. Картина уплотнения стоячей волны (о том, что такое стоячая волна, поговорим ниже — А.К.) на частоте 70 Гц показана на рис. 5. Светлые участки — это области разрежения, в которых резонанс на частоте 70 Гц на слух восприниматься не будет, а темные участки — области увеличения давления, в которых 70-герцевая составляющая звука будет четко проявляться.
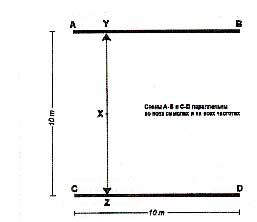
Рис. 4. Геометрически параллельные стены. Звук, исходящий из точки X, распространяется во всех направлениях, но звуковые волны, идущие в направлении точек Y и Z, отражаются по тому же пути, по которому они шли в самом начале. Они продолжают отражаться туда и обратно до тех пор, пока наконец их энергия не рассеется в стенах и воздухе.

Рис. 5. Величина поля давления, возникающего от точечного источника, расположенного между стенами, показанными на рис. 4.
А теперь изменим угол положения стен так, как показано на рис. 6, где конец одной стены придвинут к другой на 1,5 м. В этом случае у нас будут две стены с наклоном около 15° по отношению друг к другу. Хлопок в ладоши в точке X тоже породит волну, идущую в направлении точки Y, которая в отраженном виде возвратится в точку источника и продолжит свой путь к точке Z. В ту же точку Z будет направлена и прямая волна. И прямая, и отраженная волны отразятся в точке Z, но уже не в направлении точки Y, как в случае с геометрически параллельными стенами, а в направлении точки F. Затем они отразятся в направлении точки G, а потом — в направлении точки Н. В отличие от случая с геометрически параллельными стенами, показанного на рис. 4, в данном случае человек, стоящий в точке X, не будет слышать дребезжащего эха, а большая часть резонансной энергии мод помещения будет отражаться тангенциально, «проходя» в помещении по более усложненному пути. Однако в то время как высокие частоты будут отражаться по маршруту Y-Z, Z-F, F-G, G-H, осевые моды на низких частотах, у которых длина волны довольно велика, могут по-прежнему проявлять свою «живучесть». Отсюда следует, что на низких частотах стены продолжают оставаться акустически параллельными.
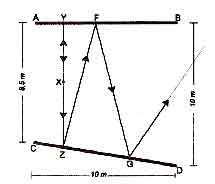
Рис.. 6. Все то же самое, что и на рис. 4, но одна отражающая поверхность сдвинута так, чтобы создать геометрическую непараллельность между поверхностями А-В и C-D. Здесь уже не будет четких эхо-сигналов наподобие тех, которые порождаются поверхностями на рис. 4, потому что отраженные сигналы не идут по одному и тому же пути. Средне- и высокочастотные звуки, распространяющиеся в направлениях точек Y и Z из точки X, идут затем по маршруту Z-F, F-G, G-H и так далее. Однако на низких частотах ситуация может едва пи отличаться от той, что показана на рис. 4.

Рис. 7. Величина поля давления, возникающего от точечного источника, расположенного между стенами, показанными на рис. 6
На рис. 7 дана картина распределения плотности стоячей волны на частоте 70 Гц для случая, продемонстрированного на рис. 6. Эта картина поразительно похожа на ту, что показана на рис. 5. Хотя из рис. 6 и следует, что непараллельное положение стен резко изменяет маршруты движения звуковых отражений, возникающих от хлопка в ладоши, и создает очень сильную дисперсию (рассеивание) на высоких частотах, на низких частотах мало что меняется. Иначе говоря, чтобы геометрическое конфигурирование помещения давало акустический результат, надо чтобы различие в длине пути, который проходит каждое последующее отражение по отношению к предыдущему, было соразмерно длине волны. Если на частоте 50 Гц длина волны составляет примерно 8 м, такой угол сдвига стен, который позволил бы добиться акустической непараллельности, возможен, вероятно, лишь в больших зданиях, размерами с концертный зал. Что же касается обычных студий звукозаписи, то у них такое конфигурирование отняло бы слишком много потенциально полезного места».
Какой вывод можно сделать из сказанного? Во-первых, геометрически параллельные поверхности в большинстве случаев являются и акустически параллельными. А это значит, что наличие первых способствует возникновению осевых резонансов, что для нас крайне нежелательно. Во-вторых, чем на более низких частотах мы стремимся достичь акустической непаралпельности, тем большей должна быть геометрическая непараллельность и площадь поверхностей.
На рис. 8 продемонстрировано влияние конфигура-ции стен (показанных на рис. 4 и 6) на акустику помещения. Как видно из графиков, на частотах выше 300 Гц геометрическая непараллельность стен заметно снижает уровень модальной энергии. Однако на частотах ниже 100 Гц заметных различий не наблюдается. Это свидетельствует о том, что в этом частотном диапазоне стены, изображенные на рис. 6, в акустическом смысле по-прежнему остаются параллельными. На частотах выше 300 Гц уровень модальной энергии уменьшается из-за того, что при геометрическом конфигурировании стен высокочастотные моды преобразуются в основном из осевых в тангенциальные. А последние не только имеют более сложную траекторию, но еще и отражаются от стен под непрямым углом, что приводит к большим потерям энергии, чем в осевых модах, которые отражаются от поверхностей перпендикулярно. Геометрическое переконфигурирование поверхностей даст эффект на частотах с такими длинами волн, когда при каждом их отражении и возвращении к исходной стене суммарное расстояние будет изменяться не менее, чем на половину длины волны, а также, естественно, и на более высоких частотах. Немного запутано? Тогда в качестве примера еще раз рассмотрим рис. 6.
Допустим, что вследствие отражений от непараллельных поверхностей звуковая волна распространяется по таким маршрутам: Y-Z -10 м; Z-F — 10,5 м; F-G -11 м; G-H-12M. При первом отражении к исходной стене звуковая волна пройдет 20,5 м (10+10,5), а при втором — 23 м (11+12). Разница при этом составит 2,5 м (23 — 20,5). Если представить расстояние в 2,5 м, как половину длины волны, то полная длина волны составит 5 м (2,5 х 2). Помня о скорости звука 340 м/с и используя формулу л = c/f получаем результат: f= c/л ; f = 340/5 ; f= 68 Гц.
На основании этих расчетов можно говорить о том, что указанная непараллельность, стен обеспечит рассеивание звуковых волн начиная от 68 Гц и выше. В этом же частотном диапазоне мы можем не опасаться возникновения осевых мод между этими поверхностями. Но вот на более низких частотах будет проявляться эффект гребенчатого фильтрования, так как звуковая волна будет поочередно проходить через усиливающую, нейтральную и ослабляющую области. Сильное гребенчатое фильтрование на низких частотах оказывает разрушающее воздействие на музыку и поэтому очень нежелательно в студиях звукозаписи, хотя в той или иной степени оно имеется во всех помещениях со звукоотражающими поверхностями. Таким образом, хотя геометрическое конфигурирование отражающих поверхностей является эффективным для подавления мод на средних и высоких частотах, на низких частотах исключительно геометрические решения обычно желаемых результатов не приносят. Поэтому здесь уже приходится дополнительно прибегать к звукопоглощению. Тем более что кроме всего прочего параллельные поверхности создают еще и повторяющийся дребезг (в просторечии — эффект «стиральной доски»), который возникает от шумов столкновения звуковой волны с отражающей поверхностью.
Ранее мы уже говорили о том, что при излучении звука между двумя параллельными поверхностями (если они не являются на 100% звукопоглощающими) неизбежно образование аксиальных мод, что приводит к формированию определенной резонансной картины. Обычное помещение в форме параллелепипеда имеет три пары таких поверхностей: две — между противоположными стенами; одна — «пол-потолок». Если предположить случай, когда помещение имеет форму куба, у которого все парные параллельные поверхности расположены друг от друга на одинаковом расстоянии, то аксиальные моды будут иметь одинаковую длину пути и обладать одинаковыми резонансами. Это приведет к сильному резонансному накоплению энергии на этих частотах. В итоге помещение будет иметь насыщенный резонансный характер со сверхмощными резонансами, разрушающими музыкальную фактуру любых озвученных в нем инструментов. Из этого можно сделать вывод, что помещение в форме куба в качестве стартовой позиции при строительстве студийного помещения является не лучшим вариантом. Проектировщик вашей студии наверняка знает формулу (известную как «график Болта», хотя им тоже следует пользоваться с некоторой осторожностью), по которой рассчитываются желательные пропорции сторон помещения, при которых обеспечивается наиболее разнообразный «ассортимент» модальных частот и, следовательно, наименее окрашенное общее звучание. Как на варианты, мы можем, к примеру, ориентироваться на пропорции 1:1,5:1,8; 1:1,59:2,52; 1:1,14:1,39; 1:1,28:2,33; 1:1,6:2,4 и т.д. Могут быть и другие пропорции. Филип Ньюэлл, например, говорит, что если помещение имеет форму коробки для обуви (в масштабе ©), то это, как правило, неплохой вариант.
Для большей наглядности рассмотрим распределение аксиальных мод в двух помещениях: одно имеет форму куба со стороной 4 м, а другое — размерами 2,5 х 4 х 5,25 м (т.е. с соблюдением пропорции 1:1,6:2,1). Высчитывать аксиальные моды мы будем по формуле:
F=340\2L
где: F — частота аксиальной моды;
L — расстояние между противоположными стенами или полом и потолком.
Упростив формулу, получим:
F=170\L
Вычислим частоты аксиальных мод для второго помещения:
5,25 м: 32,4; 64,8; 97,1; 129,5; 161,9; 194,3; 226,7; 259 Гц и т.д.
4 м: 42,5; 85; 127,5; 170; 215,5; 255 Гц и т.д.
2,5 м: 68; 136; 204; 272 Гц и т.д.
Для помещения, имеющего форму куба со стороной 4 м, частоты аксиальных мод будут следующие: 42,5; 85; 127,5; 170; 215,5; 255 Гц и т.д.
Проиллюстрируем наши расчеты графиком (рис. 14). Отобразим на рис. 14, а частоты аксиальных мод второго помещения, а на рис. 14, б — частоты аксиальных мод помещения в форме куба, Проведем кривую усредненного уровня (на рисунке -пунктирная линия). Можно заметить, что на рис. 14, а эта кривая является более гладкой, в то время как на нижнем графике «поведение» кривой усредненного уровня очень сильно подчинено энергии отдельных — удаленных друг от друга — резонансов.
Не буду спорить, в указанных графиках не учтено много моментов, например проявления резонансов на частотах тангенциальных и косых мод, а также энергия мод на всех частотах. Но если учесть, что аксиальные моды являются самыми энергоемкими и сильными, то в этой части с нашими графиками можно согласиться.

Рис.9. Распределение гармонических резонансов в помещении. На схеме показаны всплески отдельных гармонических резонансов в помещении. На участке В-С резонансы находятся недалеко друг от друга и сравнительно выравнены по уровню. «Кривая усредненного уровня» (штриховая линия) на этом участке довольно ровная. Однако на участке А-В гармонические резонансы помещения значительно удалены по частоте, а «кривая усредненного уровня» начинает изгибаться и огибать отдельные всплески и провалы в энергии резонансов. Это говорит о том, что на участке А-В звучание комнаты становится неровным, подчеркивающим одни ноты больше, чем другие. На какой частоте находится точка В — зависит от размеров помещения. Чем больше помещение, тем на более низкой частоте находится точка В. По этой причине большие комнаты обладают более равномерным звучанием из-за более низких частот разделения резонансов.
Однако в действительности все несколько сложнее. Дело в том, что вышеупомянутые модальные свойства распространяются только на пустые помещения. Как только в них устанавливается оборудование и появляются люди, равномерность распределения модальных резонансов несколько утрачивается. Тем не менее помещение с соответствующими пропорциями в качестве стартовой позиции — это намного лучше, чем помещение кубической формы. С другой стороны, эти пропорции имеют значение только для помещений среднего размера. Слишком маленьких комнат и огромных пространств размером с концертный зал они не касаются.
Частотное распределение резонансов помещения
Гармонические резонансы можно рассматривать как маршруты, которые проходят звуковые волны между отражающими поверхностями. Если звук распространяется вперед и назад и возвращается в исходную точку в той же фазе, то энергия звуковой волны на этой частоте резко возрастает, что способствует формированию резонансной стоячей волны. Соответствие расстояния между двумя поверхностями полным длинам волн является определяющим фактором проявления резонанса. Как только происходит модальное разделение, различные частотные компоненты воспроизводимой музыки начинают слышаться с разным уровнем в зависимости от того, совпадают ли они с естественными резонансами комнаты, усиливаясь ими, или нет.
Первые гармонические резонансы помещений, как правило, четко разделены по частотам, поэтому акустически необработанное помещение обладает характеристикой, более похожей на волнистую линию на рис. 10, чем на более «правильную» характеристику в виде линии «усредненной характеристики помещения» на том же графике. Гашение гармонических резонансов путем их поглощения позволяет минимизировать этот эффект, накладываемый на частотную характеристику. Вообще, демпфирование в той или иной степени необходимо для любого помещения, иначе изменение давления будет частотно- и позиционно-зависимым, а на резонансных частотах в комнате будет «зависать» энергия. Например, если частота тона бас-бочки совпадает с частотой какого-то резонанса, то вам трудно будет определить: то ли звук бас-бочки затухает медленно, то ли это медленное затухание является проявлением резонансов на этой частоте.
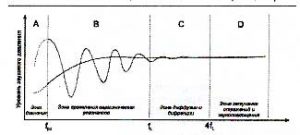
Рис.10. Частотные диапазоны с различным влиянием на акустику помещения
fpz — верхняя граница зоны давления
fl — частота разделения резонансов
В зоне давления особенности помещения не сказываются на общем звучании. Плавно закругленная сглаженная кривая является усредненной характеристикой помещения.
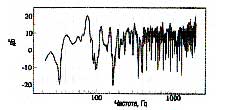
Акустически необработанное помещение вносит существенные изменения в звучание музыкальных инструментов или мониторов в этом помещении. Вспомните один из принципов фирмы FAR: «Звучание самого лучшего монитора будет настолько хорошим, насколько хороша акустика помещения, в котором он установлен». На рис. 11 показана частотная характеристика одного из таких неподготовленных помещений.
Перед тем, как заняться расчетом системы звукопоглощения, нам необходимо определить самый критичный частотный диапазон, в котором влияние гармонических резонансов является наиболее разрушительным. Поэтому сейчас мы рассмотрим зависимость поведения и проявления резонансов от частоты.
Когда гармонические резонансы перекрывают друг друга, частотная характеристика помещения будет более или менее равномерной. Но как только происходит их разделение, она становится неровной, а звучание начинает подчиняться форме отдельных резонансов (см. рис. 9). В малых комнатах это разделение начинается с более высоких частот. Из этого следует, что в больших комнатах будет наблюдаться более равномерное звучание до более низкой частоты при условии, конечно же, что все остальные характеристики комнат одинаковы.
Чтобы было более понятно, о чем идет речь, предлагаю взглянуть на рис. 10, где показано типичное частотное распределение резонансов в помещении. По характеру проявления и поведения резонансов их можно разделить на четыре частотных диапазона (зоны): давления; проявления гармонических резонансов; диффузии и дифракции (зона «перекрывания резонансов»); затухания отражений и звукопоглощения.
Наиболее проблемная с точки зрения нежелательного вмешательства в звучание гармонических резонансов — это зона проявления гармонических резонансов, которая ограничена снизу частотой fpz, а сверху частотой fL. Именно в этой зоне большей частью может происходить нежелательная окраска звука. Кстати, точка fL на рис. 10 практически соответствует точке В на рис, 9. Вычислив эти две частоты, мы сможем определить самый проблемный частотный диапазон при распределении резонансов в помещении.
Самая низкочастотная область на рис. 10 — это зона давления. Самая верхняя частота в этой зоне та, длина полуволны которой больше самого протяженного участка помещения. Эта же частота является нижней границей зоны проявления гармонических резонансов. Вычисляется эта частота очень просто:
fpz =c\Lr
где: fpz — верхняя граница (частота) зоны давления
(pressure zone — зона давления);
c — скорость звука, м/с;
Lr — самая длинная сторона комнаты, м.
Чтобы понять разницу в распределении гармонических резонансов между большими и малыми помещениями, представим, что у нас есть два помещения: большое — размерами 10мх8мх5м; малое — размерами 3 м х 2 м х 2,5 м (типичная дикторская кабина).
Итак, для большого помещения верхняя граница зоны давления составит:
fpz= 340,2×10 = 17 Гц;
для дикторской кабины:
fpz= 340,2×3= 56,7 Гц.
Ниже этих значений (т.е. в зоне давления) частотная характеристика помещения будет очень гладкой, так как в этих диапазонах резонансные явления возникать не будут. А значит частоты в зоне давления будут ниже по уровню, чем частоты в следующей зоне, где «работает» также и отраженная энергия звуковых волн.
Вычислить частоту fl более известную как «частота большой комнаты», можно по уравнению
Попытаемся вычислить частоту fl для нашей большой комнаты, принимая во внимание, что время реверберации RT60 в ней может составлять 1,2с
Теперь вычислим частоту fl для нашей дикторской кабины, учитывая, что время реверберации RT60 в ней вряд ли будет больше 0,8с
После этих вычислений можно определить частотные диапазоны, которые будут соответствовать зонам проявления гармонических резонансов для наших помещений. В большом помещении — это диапазон от 17 до 109,5 Гц; в дикторской кабине — от 56,7 до 462 Гц. Это позволяет сделать следующие выводы: во-первых, чем меньше помещение, тем выше частота верхней границы зоны давления (fpz) и частота разделения резонансов [fL}; во-вторых, чем меньше помещение, тем шире зона проявления гармонических резонансов, в которой происходит нежелательная окраска звука; в-третьих, чем меньше помещение, тем более полезные частотные диапазоны подвержены нежелательной окраске звучания собственными резонансами помещения; в самом деле, на примере дикторской кабины мы видим, что зона проявления гармонических резонансов достигает частоты 462 Гц, что практически означает проблемный диапазон вплоть до звуков второй октавы!
Вычисленные нами диапазоны частот — это те, обеспечить поглощение которых необходимо в первую очередь, если мы хотим добиться более ровной частотной характеристики помещения. В больших помещениях, где можно обустроить звукопоглощающие системы, решение этих вопросов значительно облегчается. Кроме того, в больших по размеру помещениях энергия отражений вынуждена проходить большие расстояния от источника звука до слушателя или микрофона, она более разнесена во времени и затухает гораздо сильнее.
Большие помещения имеют и большую по площади поверхность, которая может использоваться для поглощения звуковой энергии, что также является их плюсом. При определенных типах дизайна больших помещений временное и пространственное разделение сочетается с рассеивающей и поглощающей отделкой. Это создает очень приятную и совершенно равномерную акустику.
В акустическом смысле «размеры» помещения зависят от желаемой частоты распределения резонансов. Поэтому даже большая комната с равномерным распределением резонансов только до 70 Гц в акустическом смысле считается небольшой, если не расширить эту равномерность книзу до 20 Гц.
Теперь рассмотрим позиционный эффект при распределении резонансов. На рис. 12 показано распределение давления в помещении при распространении звуковой волны с частотой 70 Гц. Более темные участки -это области повышенного давления звука. Источник звука и/или слушатель, находясь в более темных областях, на частоте 70 Гц генерирует или получает звуки гораздо более сильные в отличие от более светлых областей. Если в помещении проявляется только одна паразитная резонансная частота, то выравнивание частотной характеристики возможно путем переноса либо позиции прослушивания, либо позиции источника звука, либо и того, и другого. Однако из-за разных длин волн на разных частотах (если в помещении есть две или более паразитных резонансных частот) данные схемы изменения давления в сторону повышения и в сторону понижения не будут совпадать позиционно. Выйдя из проблемной зоны на одной частоте, можно запросто попасть в проблемную зону на другой частоте.
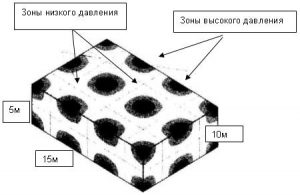
Рис. 12. Распределение резонансов в помещении на частоте 70 Гц. Темные области соответствуют зонам увеличения звукового давления, а белые — отображают зоны неизменного звукового давления. Чем больше отражательная способность поверхностей помещения, тем контрастнее будет переход от светлого к темному. Безэховая камера в этом случае показала бы более или менее однородную «серость».
Еще больше усложняет жизнь то, что каждая комната по-своему поглощает звуковую энергию в зависимости от размеров и характера акустической обработки. Разные материалы поглощают разные частоты в большей или меньшей степени. Поглощение и акустическое демпфирование определяют сипу энергии отраженного звука, а также оказывают влияние на Q (добротность) распространения энергии гармонических резонансов (рис. 13). Хотя Q и означает «добротность», но в нашем случае желательно иметь резонанс с низким Q, поскольку он менее выражен и менее назойливо действует на уши, чем резонанс с высоким Q. Поэтому помещения с сильным демпфированием и поглощением одновременно расширяют частотное содержимое резонансной энергии и уменьшают уровни резонансных пиков. Из этого следует, что звучание в звукопоглощающей комнате с низким Q будет более равномерным, чем в комнате с более твердыми стенами и гармоническими резонансами с высоким Q. Хотя во втором случае звучание будет более громким, так как такое помещение медленнее рассеивает исходящую энергию.
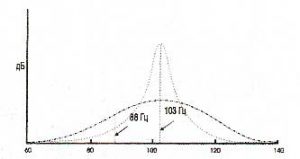
Рис. 13. Эффект демпфирования в зависимости от Q. Пунктирная линия показывает резонанс с высоким О, который сильно возбуждается при воздействии сигнала 103 Гц, но слабо реагирует на сигнал 88 Гц. Штрих-пунктирная линия показывает эффект демпфирования при снижении Q. В этом случае, возбуждение и на 88 Гц и на 103 Гц дает почти такой же уровень резонанса. Обе кривые — и штриховая и штрих-пунктирная — показывают резонансы при «частоте заводки» 103 Гц, но обе обладают одинаковым количеством общей энергии. В действительности же при обустройстве звукопоглощающих конструкций более гладкий резонанс будет содержать меньше энергии и поэтому будет ниже по уровню.
При рассмотрении вопроса позиционной зависимости при распределении резонансов необходимо остановиться и на том, что же такое стоячие волны. Этот термин употребляется часто, но смысл в него иногда вкладывается разный. Стоячие волны возникают тогда, когда две или более волны, одинаковые по частоте и типу, проходят через одну и ту же точку. Получаемая в результате картина пространственной интерференции, состоящая из областей с большой и малой амплитудой, становится «фиксированной», хотя сами волны могут перемещаться.
Резонансные стоячие волны возникают только тогда, когда, во-первых, образуется схема стоячих волн из-за взаимодействия между волной и ее отражениями от двух или более поверхностей; во-вторых, когда волна исходит от какой-то точки, отражается от одной поверхности к другой, возвращаясь в исходную точку, и снова идет в первоначальном направлении; в-третьих, когда расстояние, пройденное этой волной, в точности кратно ее длине; возвращающаяся волна усиливается, и если ее потери невелики, поле этой стоячей волны становится резонансным..
Для наглядности приведем простейший пример резонансной стоячей волны, образующейся между двумя параллельными стенами, отстоящими друг от друга на расстояние, равное половине длины волны. Волна, идущая от некоей точки к противоположной стене, отражается назад к первой стене, от которой она снова отражается в первоначальном направлении. Поскольку расстояние между стенами равно половине длины волны, то все расстояние, пройденное волной, возвратившейся в исходную точку, составляет одну длину волны. Затем волна уходит из этой же точки с такой же фазой, из-за чего на следующем цикле волна усиливается. Если изменить частоту волны или расстояние между стенами, то схема стоячей волны останется, но резонанса уже не будет.
Следует подчеркнуть, что стоячие волны существуют всегда при взаимодействии одинаковых волн, независимо от того, сложилась резонансная ситуация или нет. Поэтому употребление термина «стоячая волна» для описания только резонансных условий является не совсем правильным.
Помещения неправильной формы порождают больший разброс модальных резонансов поскольку звуковым волнам в этом случае трудно «отыскивать» пути равной длины при каждом последующем отражении. Поэтому преобладают модальные резонансы в тангенциальной или косой форме, которые, как правило, содержат меньше энергии, чем аксиальные моды, а их добротность Q является более «размазанной», так как их энергия рассеивается более широко, не позволяя им настроиться на какие-то конкретные ноты. Естественная реверберация у таких помещений обычно более сглажена и почти не имеет доминирующих частот. И все же во всех вышеперечисленных случаях самой трудно преодолимой является проблема подавления более широко разнесенных мод в самых нижних октавах слышимого диапазона. В этом диапазоне частоты имеют такую большую длину волны, что совладать с ними трудно даже с помощью наклонных стен.
Звукопоглощение
Мы уже достаточно поговорили о модах и резонансах, об их возникновении и поведении в зависимости от частоты, от позиционной зависимости, а также о том, как можно в какой-то степени управлять маршрутами мод путем изменения пропорций и геометрии помещения. Но все-таки вряд ли можно добиться приемлемых акустических условий только этими методами, поэтому без систем звукопоглощения нам не обойтись. Ведь именно звукопоглощающие поверхности отбирают значительную часть энергии звуковых волн при каждом их столкновении с этими поверхностями. Это приводит не только к значительному ослаблению энергии резонансных мод, но и к снижению добротности.
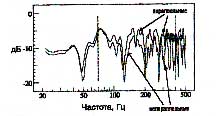
Мы выяснили, что самая проблемная область с точки зрения влияния резонансов на акустику помещения — это зона проявления гармонических резонансов (участок В на рис. 10), которая (в зависимости в основном от размеров помещения) может простираться от инфра-низких частот до нижних средних частот. К сожалению, звукопоглощение низких частот — камень преткновения для малых комнат, где нельзя применить многие системы поглощения этих частот из-за внушительных размеров таких систем. Эффективные поглотители низких частот традиционно имеют большие размеры; им требуется пространство в глубину, равное четверти длины волны самой низкой частоты, которую нужно поглощать. Если для частоты 40 Гц длина волны составляет около 8,5 м, то для поглощения звука с этой частотой и выше потребуется система поглощения глубиной более 2 м. И если в некоторых видах помещений с «живой» акустикой, предназначенных для звукозаписи, незначительное проявление резонансов может быть приемлемым и в некоторых случаях даже полезным, то в контрольных комнатах, для которых равномерность звучания является первостатейной необходимостью, их присутствие крайне нежелательно, так как это приводит к искажению условий мониторинга.
В какой-то мере нас в этой ситуации выручает то, что наши уши имеют разную чувствительность к звуковым волнам различных частот слышимого диапазона. В частности, имеет место некоторый спад чувствительности на границах слышимого диапазона, в том числе и на низких частотах. Это наглядно демонстрируется кривыми равной громкости Флетчера-Мансона (Fletcher-Munson), что можно увидеть на рис. 15. Из этого рисунка хорошо видно, как падает чувствительность слуха на пороговых значениях частотного диапазона. Так, если по кривой, которая на уровне линии 3 кГц соответствует пороговому значению 0 дБ, перейти к уровню на частоте 30 Гц, то мы получим прирост звукового давления в 60 дБ. Если же, идя по кривой, проходящей на частоте 3 кГц через точку 25 дБ, опуститься до частоты 30 Гц, то видно, что на этой частоте величина звукового давления будет составлять примерно 65 дБ.
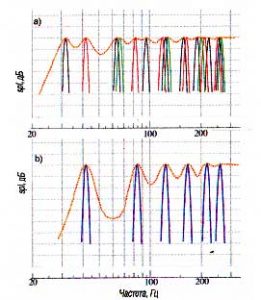
Рис.14. Распределение резонансов в помещение (аксиальные моды)
а) помещение размерами 5,25 х 4 х 2,5м;
б) помещение в форме куба со стороной 4м.
Пунктирной оранжевой линией обозначена кривая усредненного уровня

Рис. 15. Классические кривые равновеликой громкости Флетчера-Мансона, четко показывающие уровни усиления, которые необходимы для обеспечения ощущения одинаковой громкости на разных частотах
Что это значит? Во-первых, для того чтобы достичь порога слышимости, на частоте 30 Гц необходимо звуковое давление на 60 дБ (или акустическая мощность в миллион раз) больше, чем на частоте 3 кГц. Чтобы на частоте 30 Гц громкость звука соответствовала громкости 25 дБ SPL от уровня на частоте 3 кГц, нужно дополнительно еще 40 дБ (или в 10 тыс. раз большая мощность). Это говорит о том, что при низких уровнях звукового давления человеческое ухо намного чувствительнее к средним частотам, чем к низким. Во-вторых, чтобы на частоте 3 кГц повысить громкость на 25 дБ, ее нужно поднять на все 25 дБ (с 0 до 25 дБ SPL), а вот на частоте 30 Гц потребуется всего лишь 5 дБ, чтобы добиться такого же повышения субъективной громкости.
Если снова обратиться к графикам, можно сделать вывод, что 25 дБ над порогом слухового восприятия на частоте 3 кГц равноценны по громкости 5 дБ над порогом восприятия на уровне 30 Гц. Таким образом, воспринимаемая динамика звука значительно увеличивается на низких частотах. При высоких же значениях звукового давления, превышающих 100 дБ, зависимость является более линейной.
Но вернемся к нашим звукопоглощающим конструкциям. Для звукопоглощения наиболее эффективными являются многослойные конструкции из разных материалов. Дело в том, что разные материалы и варианты их компоновки поглощают звук по-разному и эффективны только в тех или иных местах и на тех или иных частотах. Так, большие фанерные панели могут очень хорошо поглощать звук, но, как правило, только на определенных частотах, поскольку обладают высоким Q (добротностью). Поглотитель с высоким Q может хорошо поглощать звук, например, на частоте 80 Гц, но почти не поглощает его на частотах 60 и 100 Гц. И если мы будем добиваться звукопоглощения с помощью таких систем (с высоким Q), то нам потребуется их много, что неизбежно будет занимать полезную площадь помещения.
Если же мы понизим Q звукопоглотителя путем добавления амортизирующих материалов, то не только понизим уровень поглощения его основной частоты, но и расширим частотный диапазон поглощения. Отсюда можно сделать вывод, что намного рациональнее добиваться звукопоглощения с помощью хорошо самортизированных систем, чем с помощью набора звукопоглоти-телей с высокой добротностью. Еще одно преимущество поглотителей с низким Q состоит в том, что резонансы затухают в них гораздо быстрее, чем в поглотителях с высоким Q. Дело в том, что резонаторы с высокой частотной избирательностью, способные быстро поглощать значительную долю энергии, имеют и оборотную «сторону медали»: они «любят» гудеть после прекращения сигнала возбуждения; другими словами, они начинают излучать вторичный призвук после импульсного возбуждения.
В следующих статьях мы более подробно рассмотрим практические приемы и механизмы звукопоглощения.
Эффективность многослойных звукопоглощающих конструкций обусловлена также тем, что звуковые волны очень «не любят» проникать из менее плотной среды в более плотную. Это явление можно проиллюстрировать двумя примерами.
Так, в книге Ф.Ньюэлла «Recording Spaces» описан случай, когда в XIX в. на склоне горы в качестве эксперимента установили две пушки — одну внизу, хотя и не у самого подножья горы, а другую — высоко, поближе к вершине. Пушки зарядили одинаковым количеством пороха, и напротив каждой пушки на склоне другой горы через ущелье выставили по наблюдателю — одного высоко, а другого пониже (рис. 16). Пушку, находящуюся ниже, не поставили на самом дне ущелья только потому, чтобы у нее не было необоснованного преимущества в плане усиления звука за счет того, что звук отражается от дна ущелья. При проведении выстрелов вспышки и дым были хорошо видны изо всех удаленных друг от друга пунктов наблюдения, а поскольку расстояние до них было известно, то предполагалось, что звук до них дойдет по истечении соответствующих интервалов времени.
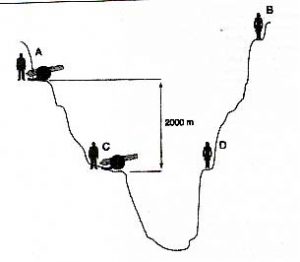
Рис. 16. Эксперимент с пушками. Два одинаковых орудия установлены в позициях А и С и заряжены одинаковым количеством пороха. При выстреле из пушки С наблюдатели в позициях А, В и D почти сразу же видят вспышку. Спустя какое-то время, соответствующее локальной скорости звука в воздухе и расстоянию до позиции С, три наблюдателя слышат выстрел из орудия. При выстреле из пушки А вспышку видят все три наблюдателя. После того как прошло соответствующее время, наблюдатель в позиции В слышит звук выстрела, тогда как наблюдатели в позициях Си D, находящиеся в более плотном воздухе, могут его так и не услышать, невзирая на го, что находятся к позиции А ближе, чем наблюдатель В.
Первым был произведен выстрел из нижней пушки. Слушатели в позициях А, В и D ожидали прибытия звука, и тот, как и предполагалось, дошел до каждой позиции в соответствующий момент времени. В каждом случае наблюдатели, услышав звук, сигнализировали флажками о его прибытии. Интенсивность звука в каждом наблюдательном пункте описывалась настолько точно, насколько это было возможно в то время, когда еще не были изобретены приборы для измерения уровня звука. Громкий звук услышал наблюдатель, находившийся внизу на противоположной стороне ущелья. Два наблюдателя, расположившиеся сверху на противоположных сторонах ущелья в позициях А и В, слышали не такой громкий, но отчетливый звук (см. рис. 16). Когда выстрелила верхняя пушка из позиции А, вспышку и дым опять-таки отчетливо видели все наблюдатели, находившиеся на расстоянии от нее, но на этот раз в позициях В, С и D. По истечении предполагавшегося отрезка времени наблюдатель в позиции В просигнализировал о том, что он отчетливо услышал звук. Но вот прошло более чем достаточно времени, за которое, как ожидалось, звук должен был бы уже дойти до позиций С и D, однако сигналов не последовало, потому что никакого звука наблюдатели, находившиеся там, не услышали.
Из этого сделали вывод, что отношение плотности воздуха в том месте, где прозвучал выстрел, к плотности воздуха в том месте, где он услышан, и есть тот фактор, который определяет, с какой силой распространяется звук. Выстрел в условиях очень плотного воздуха внизу ущелья смог легко вызвать распространение звука не только к пункту D, где плотность воздуха была такой же, но и к пунктам наблюдения в точках А и В, расположенным выше, воздух в которых имеет меньшую плотность. Что же касается верхней пушки, то хотя выстрел из нее был хорошо слышен в позиции В, которая находилась в таком же разреженном воздухе, но он решительно не смог пробиться сквозь более плотный воздух к расположенным внизу пунктам наблюдения С и D. И это несмотря на то, что позиция С находилась к позиции А ближе, чем позиция В, в которой звук был отчетливо слышен. По сравнению с более плотным воздухом внизу ущелья, разреженный воздух ближе к вершине горы создавал взрыву пороха, вылетевшему из жерла орудия, меньше сопротивления, от которого тот мог оттолкнуться. А если у взрыва меньше воздуха, от которого он может оттолкнуться, то при взрыве выполняется и меньшее количество работы. А если работы выполняется меньше, значит и звука генерируется меньше. Давление воздуха снижается почти на 100 мПа через каждые 8 м подъема над уровнем моря, а соответственно уменьшается и его плотность. Кстати, при 2000-метровой разности уровней, на которых стоят пушки на рис. 16, давление воздуха в верхних позициях А и В составляет менее 75 % от того, которое наблюдается в нижних позициях С и D.
Можно привести и более простой пример. Всем известно, что плотность воды намного больше плотности воздуха. Большинство из нас во время отдыха на море купались, ныряли, а некоторые даже погружались с аквалангом. Вспомните, как звуки шумного пляжа моментально прекращались после того, как во время ныряния или погружения с аквалангом вы (и ваши уши ©) оказывались под водой.
Поэтому если в звукопоглощающей конструкции присутствуют попеременно материалы с разной плотностью, такая конструкция способствует более эффективному звукопоглощению и особенно звукоизоляции.
Реверберация
Диффузия и дифракция.
После рассмотрения проблем, связанных с модами и резонансами, мы постепенно переходим к вопросам реверберации помещения. В недалеком прошлом реверберация считалась единственной и самой важной характеристикой закрытого помещения, предназначенного для озвучения речи или музыки. Спустя некоторое время под влиянием фундаментальных исследований акустических свойств закрытых помещений значимость реверберации поубавилась. И сейчас реверберация является одним из нескольких замеряемых параметров, по которым определяют качество звучания помещения.
Мы уже кое-что знаем о «поведении» помещений в зоне давления и в зоне распределения гармонических резонансов, которые на рис. 10 обозначены соответственно буквами А и В. Теперь вкратце рассмотрим, что же происходит в зоне диффузии и дифракции под буквой С.
Известно, что при столкновении звуковой волны с поверхностью часть ее проходит дальше, часть отражается и часть поглощается. То же можно сказать и о свете, падающем на окно. Свет попадает в помещение через оконное стекло. Если встать за окном, мы увидим на стекле свое отражение; это значит, что свет отражается туда, откуда он пришел. Через открытое окно в комнату проникает несколько больше света, чем через стекло. Разница в освещенности на улице и в помещении минус количество света, отраженного назад к своему источнику, является собственным уровнем поглощения стекла, которое преобразует энергию света в тепловую энергию. Если в окнах установить фигурное стекло, то свет будет поступать, но не будет видно его источника, а в комнату будут отбрасываться лишь смутные тени. Диффузия перемешивает дискретные источники энергии и хорошо их рассеивает. А дифракция — это искривление звуковых (световых) волн, огибающих объекты, особенно с острыми углами. Дифракция происходит и со светом, который отклоняется (дифрагирует) вокруг граней непрозрачного тепа. Дифракция световых волн, как и звуковых, зависит от частоты. При этом она создает эффект радуги, когда свет проходит сквозь узкую щель или обходит острый угол. В существовании параллелей между звуком и светом нет ничего необычного, так как оба примера связаны с распространением волн, ибо одни и те же законы распространения волн применимы и к электромагнитным световым и радиоволнам, и к акустическим звуковым волнам.
В помещении на высоких частотах звучание является комбинацией прямого звука, зеркально отраженного от твердых поверхностей, а также рассеиваемого в результате диффузии и искривленного в результате дифракции. Зеркальными называются отражения, которые возвращаются обратно в комнату дискретными и нетронутыми (как луч света, направленный в зеркало). Диффузные отражения можно сравнить с отражением луча света от листа бумаги. В нашем случае они проявляются в диапазоне, обозначенном на рис. 10 буквой С. В этом же диапазоне проявляются и эффекты дифракции (искривление волны вокруг объектов).
Таким образом, зона распределения резонансов и зона диффузии и дифракции сообща добавляют к прямому звуку следующие эффекты: дифракционную, диффузную и отраженную энергию.
А.Кравченко
По материалам Журнала «Install-Pro» №4 2003 г.